Les dividendes, il n’y a pas que ça dans la vie…
(Règle #8 d’Eric)

À votre algèbre toutes et tous, nous allons éclaircir un concept important aujourd’hui : les mathématiques savent mentir. L’investisseur doit par conséquent être prudent face aux choix qui lui sont présentés.

Par quelques propriétés algébriques simples, en ne remplaçant pas les lettres a et b par des chiffres, il est démontré dans l’encadré ci-dessous que 2 = 1. Une telle démarche, où la logique est mise de côté, équivaut à ne pas apercevoir la forêt tant nous sommes collés sur l’écorce du premier arbre à l’entrée de celle-ci. Une autre démonstration douteuse me fascine ces jours-ci. De nombreuses publicités suggèrent que les dividendes ont été les plus grands contributeurs aux rendements boursiers des 40 dernières années et qu’il est par conséquent logique d’investir dans des titres à dividendes.

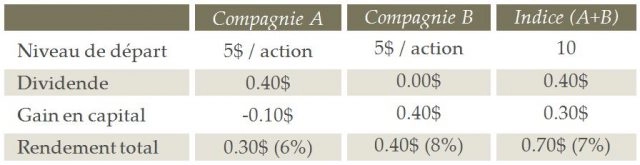
Voyons sur quelle règle d’algèbre s’appuie cette proposition. Simplifions la structure du marché en supposant qu’il n’existe que 2 compagnies dans tout le pays (le poids de chacune dans l’indice boursier sera de 50%). L’action de chaque compagnie se négocie en début d’année au même prix, soit à 5$. Le dividende ainsi que le gain (ou la perte) en capital de ces titres est illustré au tableau ci-dessous. On y résume également le rendement total des titres constituant l’indice boursier, soit 0.70$. Mais que dire de l’affirmation suivante : plus de 50% du rendement de l’indice provient du dividende? Mathématiquement, c’est vrai : le dividende de 0.40$ versé par la compagnie A représente 57.1% du rendement total de 0.70$ de l’indice. Mais prudence! Est-il rigoureux de pousser le raisonnement plus loin en suggérant qu’il soit préférable d’acheter des titres à dividende? Non. En effet, l’investisseur qui n’aurait acheté que la compagnie B (qui ne verse aucun dividende) aurait obtenu un rendement de 8% (sous forme de gain en capital) alors que le rendement total du titre de la compagnie A n’a été que de 6% en raison du recul de son action.

En analysant les tendances saisonnières des marchés financiers, nous ne devrions rejeter ni les titres à dividendes, ni ceux qui n’en versent pas. L’investisseur qui ne s’en tient qu’aux titres à dividendes s’impose une contrainte inutile qui l’empêche de tirer le maximum de « l’effet janvier », période où l’on observe régulièrement une certaine domination des titres de petite capitalisation (qui ne sont pas nécessairement réputés être de grands verseurs de dividendes). Depuis quelques années, nous observons que « l’effet janvier » débute souvent bien avant le Jour de l’An. Le quatrième trimestre est une période critique pour s’assurer que notre portefeuille est bien positionné pour la période d’hibernation des ours.

Les règles d’algèbre présentées dans l’encadré jaune plus haut sont bonnes. Mais avant de conclure que 2 est véritablement égal à 1, je dois me questionner sur la logique de la démarche que j’utilise pour le démontrer. À la dernière étape, lorsque je divise les deux côtés de l’équation par « (a – b) », je tente en quelque sorte de diviser un nombre par zéro (voir encadré ci-dessous ).

Essayez sur une calculatrice de diviser par zéro… Le résultat est erroné. Un manque de rigueur mathématique similaire m’apparaît être à l’origine de ce marketing exagéré qui suggère que les titres à dividendes rapportent davantage que les autres. À mon avis, d’autres facteurs, dont l’analyse des phénomènes boursiers saisonniers, devraient être priorisés par l’investisseur.